Every investor will tell you that compounding is the greatest force in investing. They will also tell you that at the beginning, there is very little compounding. Why should you care about something so little? Don’t you worry! I will explain to all my Level Zero Investors out there: compounding for beginners.
What is Compounding?
The best way I can describe compounding is when you take the gains you’ve made from your investment, and you make more gains off of those gains.
I am a visual/practical example learner, so let’s apply some numbers that can explain compounding.
You start with an initial investment of $10, with a goal of growing by 10% each year. After Year 1, 10% would be $1, and now we have $11. Wanting to grow by another 10% the next year, instead of gaining another $1.00, we actually grow by $1.10, bringing our total to $12.10.
Why was the gain higher in Year 2 versus Year 1? That 10% return was applied to $11, not $10.
Compounding focuses on the GAINS. With a consistent rate of return, the value subject to the 10% growth undergoes a shift. Each subsequent year, the investment value increases, and therefore the gains also increase.
Gaining off the Gains.
Compounding for Beginners – Focus on the Gains!
Continuing on from our previous example, I want to focus specifically on the gains from each year.
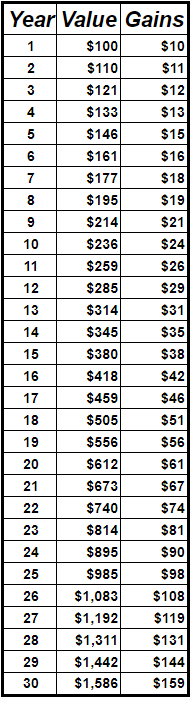
Expanding on the example above, I put the data into a table and graph, remember I’m a visual learner.
Starting with $100 this time, looking at Year 1 and Year 2, our gains were $10 and $11 respectively. For the first 10 years, there was little change between the year-over-year gains, increasing by a little over a dollar each year. Not very exciting, I get it.
However, by Year 9, our gains are now DOUBLE compared to when we started, increasing from $10 to $21.
As you start scrolling down the table as the years grow, that $10 gain we saw in Year 1 turns into $108 in Year 26. At this point, you are now gaining more per year than you initially invested!
Compounding takes time. Compounding is NOT linear.
That is the power of compounding. One day, your gains will outgrow your initial investment and that is when the snowball really starts to pick up speed!
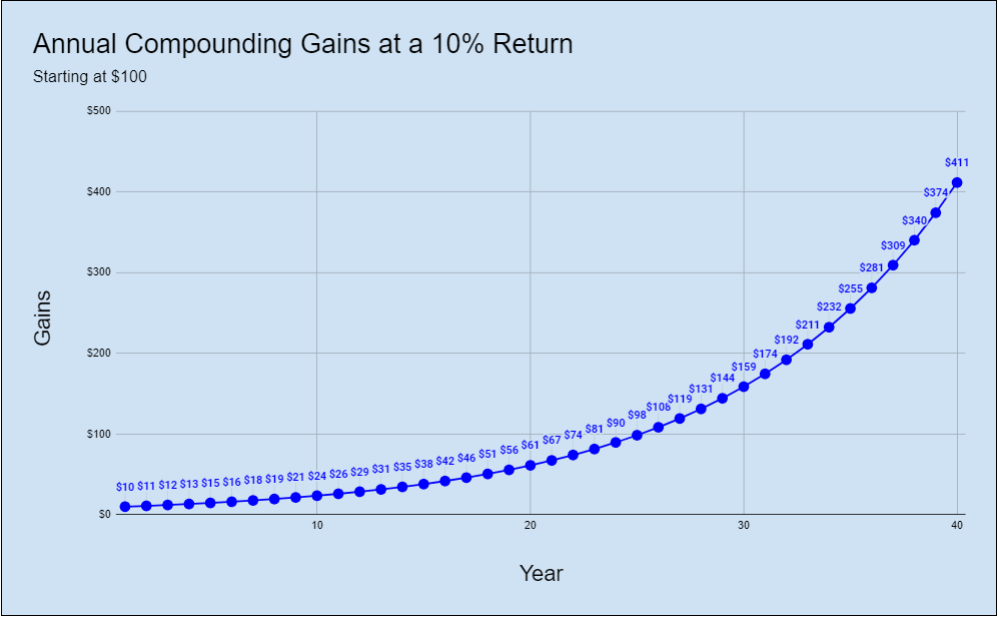
While looking at the table of actual values is great, I need more visualization. Below is a graphical representation of the table above. I also added an extra 10 years of compounding to better visualize the growth.
As described, the first 10 years don’t seem like much. But as time passes, the change in annual gains goes from $1 to $2 to $4 to $10 and so on! By Year 20, and especially after Year 30, you start to see that line skyrocket upwards.
This is the goal for every investor. As you keep investing and you keep giving your investments more time to grow, it will start to grow on its own. That is how wealth is created.
8 Examples of Compounding for Beginners
By now, you’ll see how compounding grows exponentially over time. But I want to give you a couple more examples to help illustrate how compounding works.
Hydra – A Compounding Head-Ache
A Hydra, in Greek mythology, was a giant snake-like monster with multiple heads. This monster is unique because if you were to fight it, every time you chop off a head two more would take its place.
A favorite (and underrated movie) of mine, Disney’s Hercules movie, did a great job bringing the Hydra to life in an epic battle. Hercules battled the monster, chopping head after head after head…until there were too many heads to battle.
In this case, compounding was against Hercules. One head was battle. Tens to hundreds of heads was a war. But we can see how this doubling effect started slowly at first but quickly grew out of hand.
Doubling a Penny Every Day for a Month
Sticking with a doubling theme, if someone were to ask you if you wanted $1 million right now, or a penny doubled for the next 31 days…what would you choose?
While $1,000,000 is much greater than $0.01, you would be remiss to see the power of compounding. Below is a calendar, where if you started with a penny on Sunday and doubled each day till the 31st, you’ll see that penny turn into $10.7 million!!!
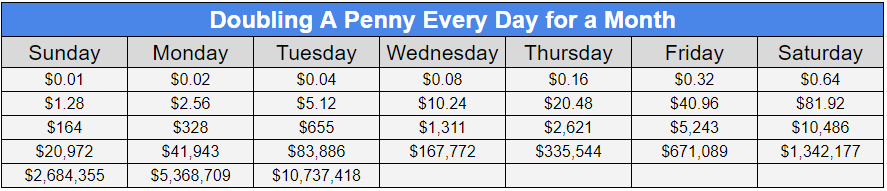
At the beginning, compounding doesn’t do much. It took till day 8 to reach over $1, but the growth afterward boosted that penny to over $10 million.
Hockey Stick
While we talk about compounding to have exponential growth, small at first then steep later on…what would be the best way to describe that shape?
A hockey stick.
A hockey stick consists of two main parts: the shaft and the blade. The shaft is the long straight piece that the player holds, while the blade is what is used to hit the puck.
Relating this to compounding, the flat shaft is the start of compounding, flat with little growth. But when the shaft meets the blade, that’s when your investment takes off and starts to increase rapidly.
Snowball Rolling Down a Hill
Have you ever seen those cartoons where the character throws a snowball down a hill and it grows like crazy…usually crushing or absorbing another character on its path down the hill? This is another great example of how compounding works.
The initial investment, the snowball that fits in the palm of your hand, is tossed down the hill. Little by little, that snowball gathers more snow. Eventually, that snowball grows into a giant snowball, becoming an unstoppable force.
Investing is the same way. You take your initial investment and give it time to grow. As it builds momentum, it starts growing on its own. The growth becomes more than what you initially invested.
The 8th Wonder of the World – A Genius Understands its Power
Albert Einstein, a genius, totally understood the power of compounding. He had this famous quote saying:
“Compound interest is the eighth wonder of the world. He who understands it, earns it; he who doesn’t, pays it.”
-Albert Einstein
It doesn’t take a genius to understand the power of compounding. Go out and earn it for yourself!
Benjamin Franklin Left a Compounding Nest Egg for Two Cities
When Benjamin Franklin died in 1790, he left Boston and Philadelphia 1,000 pounds each (around $4,000 to $5,000). Each city was to create a fund that would grow for the next 200 years (Franklin’s Philadelphia and Boston Trust Fund). The needy could also borrow from the fund at 5 percent interest; he was interested in helping people learn trades.
After 200 years, these accounts grew to $2.25 million (Philadelphia) and $5 million (Boston).
Why did Franklin do it? To help people understand the importance of compound interest.
“A penny saved is a penny earned.”
-Benjamin Franklin
To read more about Benjamin Franklin’s compounding story, read What Ben Franklin Can Teach You About the Power of Compound Interest.
Compounding Occurrs in Nature – A Sunflower
I had to find an example of compound interest in occurred in nature. And the example I wanted to use was the sunflower.
For starters, it’s my wife’s favorite flower. Before we got married we were renting this house and thought it would be a great idea to plant some sunflower seeds in the front yard garden bed. Boy did those things grow like crazy! This little tiny house we were staying in, had these MASSIVE sunflowers all in the front yard. The best part, in the fall, I took out all the seeds from the flowers and we ate them.
Not gonna lie, there were a TON of seeds. A single sunflower can produce up to 1,000 to 2,000 seeds. Imagine a field of sunflowers. You start with one sunflower. Then after the first year, they drop those 1,000 seeds…and next year you get 1,000 sunflowers…(I know not all of them will germinate, but let’s have fun) Then the next year those 1,000 sunflowers drop another 1,000 seeds…and now you’re up to 1,000,000 sunflowers.
We can learn math from nature. Nature is beautiful.
Compound Interest Calculator – The Most Fun You’ll Ever Have with Math
The last example of compounding for beginners is simply running the numbers using a compound interest calculator.
Many of these calculators exist out there, but my bread and butter is the compound interest calculator from Investor.gov.
Below is a snapshot of the 4-steps you need to run the calculator.
- Initial Investment – How much you are starting with
- Monthly Contribution & Length of Time – How much you plan on adding each month and how many years you’ll allow this investment to compound.
- Interest Rate – How much you expect to grow each year.
- Compounding Frequency – How often you expect compounding to occur.
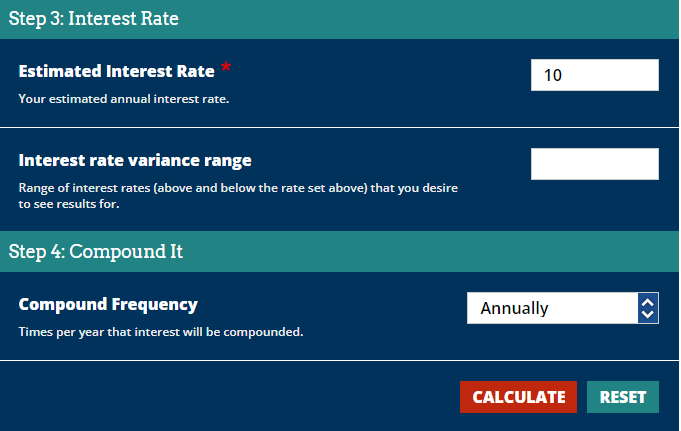
In my example above, I am starting from zero. However, for the next 40 years, I plan on investing $200 per month into an S&P 500 index fund. The S&P 500 has returned around 10% annually since WW2.
After you hit “Calculate” the results will show below.
Like our hockey stick example, you’ll see the future value (red line) look almost flat for the first 15-20 years. But that growth really starts to kick in afterward, reaching over $1,000,000 by year 40.
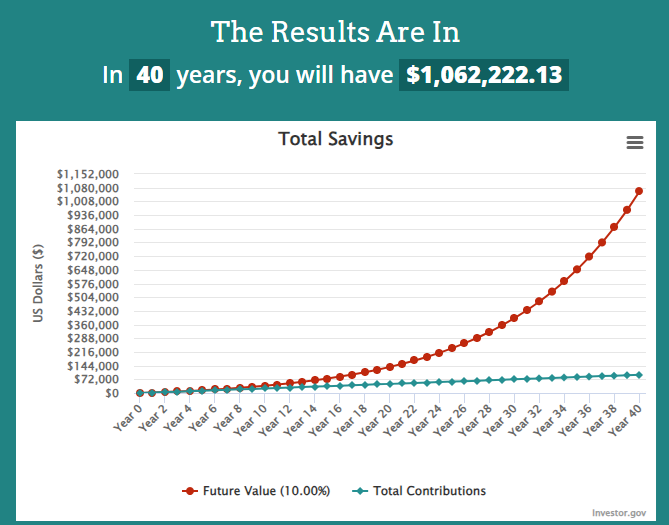
This calculator is great because it allows you to play with the numbers. Maybe you want to increase your monthly contribution? Or you’re starting with an initial investment of $10,000. What if retirement is only 20 years away? You could change the inputs to determine how much you’d need to invest to reach a certain target number.
So simple, yet so powerful!
What Next? You Want to Start Compounding, So Learn about the S&P 500!
In our last example of compounding, I used the S&P 500 to reference what to invest in. Why did I choose that? Because there is a very long history and track record of what the S&P 500 has done.
I highly recommend that any beginner, any level zero investor, read more about the What is the S&P 500.
Thanks for reading! Which is your favorite compounding example? Did I miss one? Leave a comment below and let me know!
Disclaimer
Levelzeroinvestor.com is not a registered investment, legal or tax advisor or a broker/dealer. All investments / financial opinions expressed by Levelzeroinvestor.com are from the personal research and experience of the owner of the site and are intended as educational material. Although best efforts are made to ensure that all information is accurate and up to date, occasionally unintended errors and misprints may occur.
Great examples to illustrate the power of compounding. My favourite is the hockey stick, which looks so much like the exponential curve.
Let’s continue to earn compound interest instead of pay it. 🙌
Бытовки под ключ: быстрая доставка и монтаж на участке
купить металлическую бытовку bytovki-moskva0.ru/metallicheskie-bytovki .
Готовые каркасные дома под ключ: идеальное решение для вашего участка
каркасный дом под ключ в спб http://www.karkasnye-doma-spb1.ru/ .